优化算法的功能就是改善训练方式,来最小化(最大化)损失函数 模型内部有些参数,是用来计算测试集中目标值 Y 的真实值和预测值的偏差,基于这些参数,就形成了损失函数E(x)。 比如说,权重( ω ω ω)和偏差(b)就是这样的内部参数,一般用于计算输出值,在训练神经网络模型时起到主要作用。 在有效地训练模型并产生准确结果时,模型的内部参数起到了非常重要的作用。这也是为什么我们应该用各种优化策略和算法,来更新和计算影响模型训练和模型输出的网络参数,使其逼近或达到最优值。 优化算法分为两大类 这种算法使用各参数的梯度值来最小化或最大化损失函数,最常用的一阶优化算法是梯度下降 函数梯度:导数 dy / dx 的多变量表达式,用来表示y相对于x的瞬时变化率。往往为了计算多变量函数的导数时,会用梯度取代导数,并使用偏导数来计算梯度。梯度和导数之间的一个主要区别是函数的梯度形成了一个向量场。 因此,对单变量函数,使用导数来分析;而梯度是基于多变量函数而产生的。更多理论细节在这里不再进行详细解释。 经典的随机梯度下降法(Stochastic Gradient Descent,简称SGD)是神经网络训练的基本算法,即每次批处理训练时计算网络误差并作误差反向传播,后根据一阶梯度信息对参数进行更新,其更新策略可表示为: 其中,一阶梯度信息 ? ω t
abla{\omega_t} ?ωt? 完全依赖与当前批数据在网络目标函数上的误差,故可以将学习率 η \eta η理解为当前批的梯度对网络整体参数更新的影响程度。 经典的随机梯度下降是最常见的神经网络优化方法,收敛效果稳定,不过收敛速度慢。 基于动量的随机梯度下降算法是在SGD的基础上加速学习,特别是处理高曲率,小但一致的梯度或是带噪声的梯度。 带动量的随机梯度下降算法不再沿着梯度的方向,而是沿着速度的方向,因此会快很多(速度的方向也就是指之前累计的梯度方向) 带动量的SGD不容易出现局部极小值和鞍点,因为虽然这两者附近的梯度比较小,但是还有之前累计的速度向量,这能够帮助我们越过鞍点,继续训练随机梯度下降法
ω t=ω t ? 1 ? η ? ? ω t ) \omega_t=\omega_{t-1 }- \eta *
abla{\omega_t}) ωt?=ωt?1??η??ωt?)
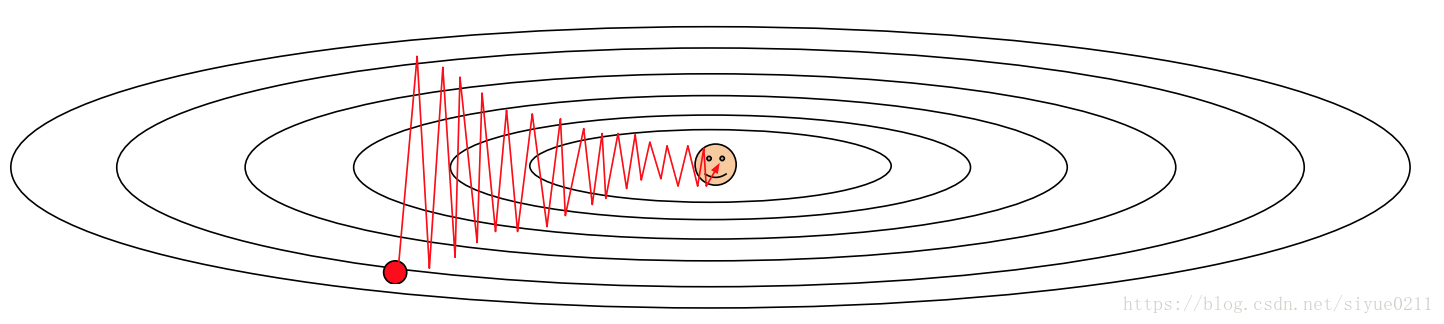
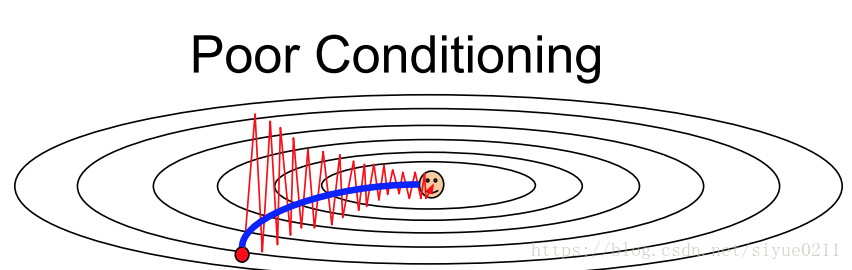
因为梯度方向和较小值方向并不是在一条直线上,所以之字形的来回迭代
而且随机梯度下降算法容易陷在局部最小值或者鞍点,局部最小值在低维度的时候看着比较严重,但是在高纬度时鞍点才是核心问题。因为高纬度的时候,参数就有上千个,不同参数的变化很容易造成某些纬度损失增大,某些纬度损失减小,总的损失很小
创客课程开发的每个主题课程需要基于现实情景,设置学习探究任务,通过问题研究、任务...
创客空间建设 能够给人们分享各种乐趣,通过电脑,技术,科学,艺术结合,设计创造一...
在了解创客教育之前,我们首先了解下何为创客。创客是一群喜欢或享受创新的人。创客跨...
STEAM教育是对传统教育的提升,它是基于自然学校方式的功能性框架,可以适合各类...